Polarized light has three fundamental characteristics: wavelength, intensity, and polarization. The wavelength of light is easy to understand. For example, the wavelength range of visible light is distributed between 380 and 780 nm. The intensity of light is also easy to grasp; whether a beam of light is strong or weak can be characterized by its power. In contrast, the polarization characteristic of light describes the vibration direction of the electric field vector, which is neither visible nor tangible, making it generally harder to understand.
However, in practice, the polarization characteristic of light is equally important and has widespread applications in daily life. For instance, the liquid crystal displays (LCDs) we look at every day use polarization technology to achieve color display and contrast adjustment. The 3D glasses we wear when watching 3D movies in theaters also utilize light polarization.
For professionals working in optics, having a thorough understanding of polarization phenomena and applying this knowledge in practical optical systems can be very beneficial for the success of products and projects. Therefore, starting from this article, we will introduce the concept of light polarization in an easy-to-understand manner, enabling everyone to gain a deep understanding of polarization and apply it more effectively in their work.
Since the concepts involved are quite numerous, we will introduce them step by step in several subsections.
We know that light is a type of electromagnetic wave. As shown in the figure below, an electromagnetic wave consists of an electric field (E) and a magnetic field (B) that are perpendicular to each other. These two fields oscillate in their respective directions and propagate transversely along the direction of propagation (Z).
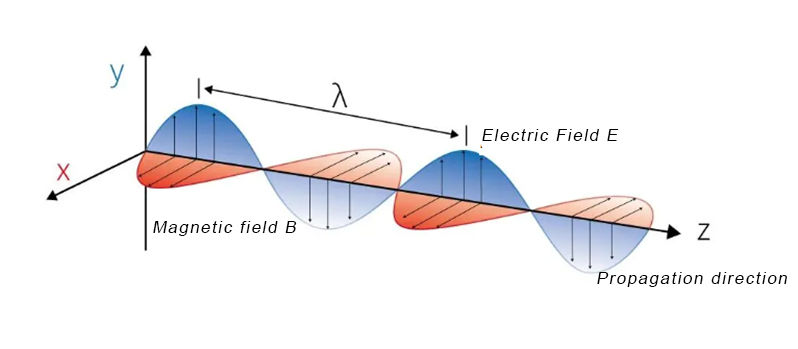
In an electromagnetic wave, the electric field vector (E) and the magnetic field vector (B) oscillate perpendicularly to each other and to the direction of wave propagation (Z). The polarization of light specifically refers to the orientation and behavior of the electric field vector (E) as the wave propagates.
Understanding the concept of polarization is crucial because it affects how light interacts with materials and how it can be manipulated for various applications. For instance, polarized light can be used to reduce glare, enhance contrast in imaging systems, and enable 3D visualization in movies.
In the following sections, we will delve deeper into the different types of polarization, how they can be generated and manipulated, and the practical applications by optical component manufacturers in everyday life and advanced optical systems.
Because the electric field and magnetic field are perpendicular to each other, have the same phase, and propagate in the same direction, in practice, the polarization of light is described by analyzing the oscillation of the electric field. As shown in the figure below, the electric field vector ( \mathbf{E} ) can be decomposed into components ( E_x ) and ( E_y ). Polarization refers to the distribution of the oscillation directions of the electric field components ( E_x ) and ( E_y ) over time and space.
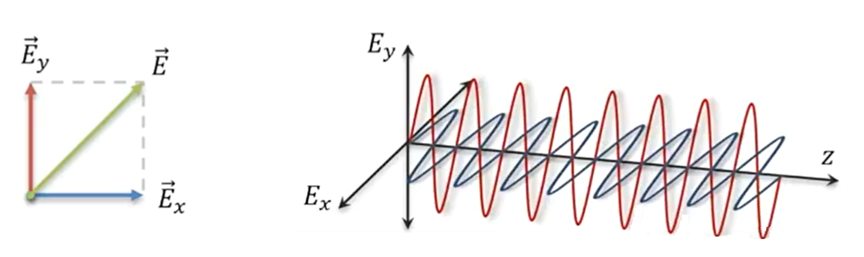
In more detail, the electric field vector ( \mathbf{E} ) can be expressed as: [ \mathbf{E} = E_x \hat{i} + E_y \hat{j} ] where ( \hat{i} ) and ( \hat{j} ) are unit vectors in the x and y directions, respectively.
The behavior of ( E_x ) and ( E_y ) over time and space determines the type of polarization:
Linear Polarization: If ( E_x ) and ( E_y ) are in phase (or out of phase by 180 degrees), the electric field vector ( \mathbf{E} ) oscillates in a single plane. The angle of this plane depends on the relative magnitudes of ( E_x ) and ( E_y ).
Circular Polarization: If ( E_x ) and ( E_y ) have the same amplitude but are 90 degrees out of phase, the electric field vector ( \mathbf{E} ) traces out a circle in the plane perpendicular to the direction of propagation. The direction of rotation (clockwise or counterclockwise) determines whether it is right-handed or left-handed circular polarization.
Elliptical Polarization: If ( E_x ) and ( E_y ) have different amplitudes and/or are out of phase by an arbitrary amount other than 0 or 90 degrees, the electric field vector ( \mathbf{E} ) traces out an ellipse. This is the most general form of polarization.
By understanding how the electric field components ( E_x ) and ( E_y ) oscillate, we can fully describe the polarization state of light. This understanding is essential for designing and analyzing optical systems that rely on polarization, such as polarizing filters, liquid crystal displays, and various types of sensors and communication devices.